Practica 4-Velarde

EJEMPLOS.

1.-  Jamestown Steel Company fabrica y arma escritorios y otros muebles para oficina en diferentes plantas en el oeste del estado de Nueva York. La producción semanal del escritorio modelo A325 en la planta de Fredonia tiene una distribución normal, con una media de 200 y una desviación estándar de 16. Hace poco, con motivo de la expansión del mercado, se introdujeron nuevos métodos de producción y se contrató a más empleados. El vicepresidente de fabricación pretende investigar si hubo algún cambio en la producción semanal del escritorio modelo A325. En otras palabras, ¿la cantidad media de escritorios que se produjeron en la planta de Fredonia es diferente de 200 escritorios semanales con un nivel de significancia de 0.01?

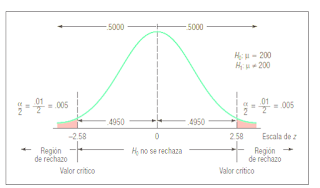
Como 1.55 no cae en la región de rechazo, H0 no se rechaza. La conclusión es: la media de la población no es distinta de 200. Por lo tanto, se informa al vicepresidente de fabricación que la evidencia de la muestra no indica que la tasa de producción en la planta de Fredonia haya cambiado de 200 semanales.

2.-1)      La longitud media de una pequeña barra de contrapeso es de 43 milímetros. Al supervisor de producción le preocupa que hayan cambiado los ajustes de la máquina de producción de barras. Solicita una investigación al departamento de ingeniería, que selecciona una muestra aleatoria de 12 barras y las mide. Los resultados aparecen en seguida, expresados en milímetros.

¿Es razonable concluir que cambió la longitud media de las barras? Utilice el nivel de significancia

0.02.

La hipótesis alternativa no señala una dirección, así que se trata de una prueba de dos colas. Hay 11 grados de libertad, que se calculan por medio de n=12 -1 = 11. El valor t es de 2.718, en el caso de una prueba de dos colas con un nivel de significancia de 0.02 y 11 grados de libertad. La regla de decisión es: se rechaza la hipótesis nula si el valor calculado de t se localiza a la izquierda de -2.718 o a la derecha de 2.718.

La hipótesis nula que afirma que la media poblacional es de 43 milímetros se rechaza porque el valor calculado de t de -2.913 se encuentra en el área a la izquierda de -2.718. Se  acepta la hipótesis alternativa y se concluye que la media poblacional no es de 43 milímetros.

3.-

EJERCICIOS

1,-

2,-

3,-

Práctica 4 - Ramos

Ejemplo 1

Se ha tomado una muestra aleatoria de 50 artículos producidos por una industria y se obtuvo que el peso de la media muestral fue de 165gr con una desviacion estandar de 40gr. Encuentre el mayor error en la estimación de la media poblacional, con una confianza de 95%

Ejercicio 1, página 347

Ejemplo 2

Se conoce que la varianza de una poblacion es 20. Determine cual debe ser el tamaño de la muestra para que el error máximo en la estimación de la media poblacional mediante la media muestral no exceda de 1 con una probabilidad de 99%

Ejercicio 9, página 352

Ejemplo 3

Se ha tomado una muestra aleatoria de 50 artículos producidos por una industria y se obtuvo que la media muestral del peso de los artículos fue 165 gr. con una desviacion estándar de 40 gr. Encuentre un intervalo para la media poblacional, con un nivel de confianza de 98%

Ejercicio 15, página 355

Practica 3-Distribucion de probabilidad hipergeométrica.

Distribución de probabilidad hipergeométrica.

Cuando la probabilidad de éxito no es la misma en todos los ensayos cuando se realiza un muestreo sin reemplazo en una población relativamente pequeña, no debe aplicarse la distribución binomial. En lugar de ésta se aplica la distribución hipergeométrica. Por lo tanto, 1) si se selecciona una muestra de una población finita sin reemplazo y 2) si el tamaño de la muestra n es mayor que 5% del tamaño de la población N, se aplica la distribución hipergeométrica para determinar la probabilidad de un número específico de éxitos o fracasos. Esto resulta especialmente apropiado cuando el tamaño de la población es pequeño.

La fórmula de la distribución de probabilidad hipergeométrica es la siguiente:

donde:

N representa el tamaño de la población.

S es el número de éxitos en la población.

x es el número de éxitos en la muestra; éste puede asumir los valores 0, 1, 2, 3…

n es el tamaño de la muestra o el número de ensayos.

C es el símbolo de combinación.

En resumen, una distribución de probabilidad hipergeométrica tiene las siguientes características:

1. Los resultados de cada ensayo de un experimento se clasifican en dos categorías exclusivas: éxito o fracaso.

2. La variable aleatoria es el número de éxitos de un número fijo de ensayos.

3. Los ensayos no son independientes.

4. Los muestreos se realizan con una población finita sin reemplazo y n/N > 0.05. Por lo tanto, la probabilidad de éxito cambia en cada ensayo.

Ejemplo

Play Time Toys, Inc., tiene 50 empleados en el departamento de ensamblado. Sólo cuarenta de ellos pertenecen al sindicato. Se eligen al azar cinco empleados para formar un comité que hablará con la empresa sobre los horarios de inicio de los turnos. ¿Cuál es la probabilidad de que cuatro de los cinco empleados elegidos para formar parte del comité pertenezcan a un sindicato?

En este caso, la población consiste en los 50 empleados del departamento de ensamblado. Sólo se puede elegir una vez a un empleado para formar parte del comité. De ahí que el muestreo se lleve a cabo sin reemplazo. Por lo tanto, en cada ensayo cambia la probabilidad de elegir a un empleado sindicalizado. La distribución hipergeométrica es adecuada para determinar la probabilidad. En este problema,

·         N es igual a 50, el número de empleados.

·         S tiene un valor de 40, el número de empleados sindicalizados.

·         x es igual a 4, el número de empleados sindicalizados elegidos.

·         n vale 5, el número de empleados elegidos.

Se desea calcular la probabilidad de que 4 de los 5 miembros del comité sean sindicalizados. Al sustituir estos valores en la fórmula, se obtiene:

Practica 3-Distribucion de probabilidad normal estandar.

Distribución de probabilidad normal estándar.

El número de distribuciones normales es ilimitado y cada una posee diferentes medias y desviaciones estándar. Es posible proporcionar tablas de probabilidad de distribuciones discretas, como la binomial y la de Poisson, es imposible elaborar tablas de una infinidad de distribuciones normales. Cualquier distribución normal puede convertirse en una distribución de probabilidad normal estándar si se resta la media de cada observación y se divide esta diferencia entre la desviación estándar. Los resultados reciben el nombre de valores Z o valores tipificados.

Definición

Z: Distancia con signo entre un valor seleccionado, designado X, y la media , dividida entre la desviación estándar.

Donde X: Valor de cualquier observación y medición.

Área bajo la curva normal.

Tabla de frecuencias.

Ejemplo 1.

Calcular la probabilidad de que las cajas de Sugar Yummies pesen entre 283 y 285.4 gramos. El peso de la caja de Sugar Yummies tiene una distribución normal con una media de 283 gramos y desviación estándar de 1.6 gramos.

Ejemplo 2.

Los ingresos semanales de los supervisores de turno de la industria del vidrio se rigen por una distribución de probabilidad normal con una media de $1 000 y una desviación estándar de $100. ¿Cuál es el valor z del ingreso X de un supervisor que percibe $1 100 semanales? ¿Y de un supervisor que gana $900 semanales?

El valor de z de 1 indica que un ingreso semanal de $1100 esta a una desviación estándar por encima de la media, y un valor de -1 muestra que un ingreso de $900 está a una desviación estándar por debajo de la media. Observe que ambos ingresos se encuentran a la misma distancia de la media.

Practica unidad 3-Distribución de probabilidad uniforme

Distribución de probabilidad uniforme

La distribución uniforme tiene forma rectangular y queda definida por valores mínimos y máximos. La distribución de probabilidad uniforme es, tal vez, la distribución más simple de una variable aleatoria continua.

En la siguiente figura aparece una distribución uniforme. La forma de la distribución es rectangular y posee un valor mínimo a y un máximo b. Observe, asimismo, que la altura de la distribución es constante o uniforme para todos los valores entre a y b.

Media

Desviación estándar

Probabilidad de la distribución uniforme

Ejemplo 1

El precio de cierre de una acción común de Schnur Sporting Goods Inc., está uniformemente dis- tribuido entre $20 y $30 por acción. ¿Cuál es la probabilidad de que el precio de la acción sea:

·         mayor a $27

a = 27

b = 30

P(x) = 1/(30-27)

P(x) = .3

Ejemplo 2

Una distribución uniforme se define en el intervalo de 2 a 5.

·         Calcule la probabilidad de un valor mayor que 2.6.

a = 2.6

b = 5

P(x) = 1/(5-2.6)

P(x) = .41

Ejercicio

Práctica unidad 3 - Distribucion binomial

Esta distribución corresponde a experimentos con características similares a un experimento de Bernoulli, pero ahora es de interés la variable aleatoria relacionada con la cantidad de “éxitos” que se obtienen en el experimento.

Características de un experimento binomial

      a)      La cantidad de ensayos que se realiza es finita. Sea esta cantidad n

      b)      Cada ensayo tiene únicamente dos resultados posibles: “éxito” o “fracaso”

      c)       Todos los ensayos realizados son independientes

      d)      La probabilidad de “éxito” en cada ensayo permanece constante. Sea este valor p.

Definición

Sean X: variable aleatoria discreta cuyo valor representa la cantidad de ensayos considerados “’éxitos” en una serie de n ensayos realizados.

x = 0, 1, .., n, valores que puede tomar X

p: valor de la probabilidad de que cada resultado sea “éxito”

Entonces, la distribución de probabilidad X es:

La media es:

Y la varianza es:

Ejemplo 1.

Se realizan 8 lanzamientos de un dado. Calcule la probabilidad de obtener 4 veces el número 4.

Ejemplo 2.

Una fábrica tiene una norma de control de calidad consistente en elegir al azar diariamente 20 artículos producidos y determinar el número de unidades defectuosas. Si hay dos o más artículos defectuosos la fabricación se detiene para inspección de los equipos. Se conoce por experiencia que la probabilidad de que un artículo producido sea defectuoso es 5%. Encuentre la probabilidad de que en cualquier día la producción se detenga al aplicar esta norma de control de calidad.

Ejercicio: